受験情報

「五ツ木模試って聞いたことあるけど何するの?」「五ツ木模試って受けたほうがいい?」
などと、疑問に思っている方も少なくないでしょう。五ツ木模試とは、延べ17万人もの人が受験している模擬テスト会のことです。かれこれ50年以上にわたって実施してきている五ツ木模試。豊富なデータに基づいた分析力と、その精度の高い志望校判定は、進路を決める重要な参考資料として役立てられるでしょう。今回は五ツ木模試についてまとめてみました。
目次
実施地域
大阪府、兵庫県、奈良県、京都府、和歌山県、三重県
年間実施日程
日程は予め発表されています。2020年度の実施日程(予定)は以下の通りです。
【中3生】
- 第1回 5月17日(日)
- 第2回 6月14日(日)
- 第3回 7月12日(日)
- 第4回 9月13日(日)
- 第5回 10月11日(日)
- 第6回 11月15日(日)
- 第7回(※特別回) 12月13日(日)
- 第8回 1月24日(日)
※特別回…実際の志望校(専願・併願の私立高校)を会場として受験することができます。
参考として、2015年度では、大阪府、兵庫県、奈良県、京都府、和歌山県の全105の高校が会場として選択できました。
志望校を決定していく時期である、第4回、第5回、第6回が、年間を通して受験者数が多くなります。
その中でも、第6回目が、最も受験者数が多くなります。
参考までに2019年度の実績をご紹介します。
- 9月(第4回)30703人
- 10月(第5回)31080人
- 11月(第6回)51618人
【中1・2年生】
中学1・2年生向けは「学力テスト」があります。
2019年度実施日程
- 第1回 9月15日(日)
- 第2回 2月2日(日)
【受験者数が多い方が良いの?】
受験者数は多い方が良いです。
単純に母数が多い方が、サンプルが多く取れますので、信憑性が高まります。
例えば、2019年度の11月模試で、枚方高校(普通科)を志望校判定で希望した人数は 人でした。
実際、2019年度入試における、普通科の第一志望者数は364人でした。 ちなみに、枚方高校(普通科)の募集定員は240人です。
このように、本番よりも多い受験者数になることもありますので、より現実的に、「集団の中での自分自身の位置」が分かってきます。
【中学1・2年生の内から受けた方が良いの?】
模試を受ける目的が明確であれば、メリットはあると思います。これは中学3年生にも言えることですが、模試を受けるだけでは、あまり意味がありません。
確かに、学校のテストだけでは測れない偏差値が分かり、集団の中での自分の位置を知ることができるだけでも一つ収穫だと思います。
しかし大切なことは、自分自身の苦手分野をしっかりと把握し、復習すること、学力アップに活かすことです。
申込方法
【料金】4,400円(税込み)※当日申込は5,400円
次の3つの方法で申し込みができます。
1. 最寄りの取扱店(書店)で購入
お近くの指定取扱店(書店)で受験票を購入できます。
2. オンライン申込
パソコンやスマートフォンで専用サイトにアクセスして、申し込み、購入ができます。
3. 団体申込
通っている塾で団体申し込みをする場合です。詳細は塾にお問い合わせください。
実施会場
個人申込の場合は、席に余裕のある会場であれば、どこでも選ぶことが可能です。
団体申し込みの場合は、予め指定された会場で実施されます。
実施会場については、私立の高校や大学が会場になっていることがほとんどです。
例として、寝屋川市在住の中学生が受験する場合の主な会場をご紹介します。
・大阪電気通信大学高校 (京阪本線寝屋川市駅東 徒歩15分)
・大阪電気通信大学 (京阪本線・地下鉄谷町線守口駅東 徒歩10分)
・大阪国際大和田高校 (京阪本線大和田駅 徒歩7分)
・大阪産業大学附属高校 (京阪本線関目駅南東 徒歩15分)
・常翔啓光学園高校 (京阪交野線宮之阪駅北東 徒歩7分)
出題範囲について
出題範囲はあります。
ただし基本的に、「受験する時点での、それまでに学校で習った範囲全て」と思ってください。
例として、中3生の2015年第4回実施の出題範囲をご紹介します。

現学年で習う範囲に関しては、地域や学校により、学校進度に差があることが考慮されています。例えば数学では、「2次方程式」の記載がありません。
ただし、9月の時点で、通っている中学校では、既に習っている可能性は十分あります。
つまり、「現学年の出題範囲はどこまでか」については、参考として確認しておいた方が良いと言えます。
この出題範囲は、五ツ木書房の公式HPでも公開されますし、受験票を購入する際に貰えます。
結果(個人成績表)について
受験後は、「個人成績表」が送付されます。手元に届くのは、実施日から約2週間程度かかります。以下の内容が記載されます。(両面 A3、2枚)
①今回の成績 各科目100点満点です。偏差値も記載されます。
②教科バランス 今回と前回の各科目の偏差値をレーダーチャートで示したものです。
科目間の実力の違いを見ることができます。レーダーチャートとは、以下の様な表です。
【例】
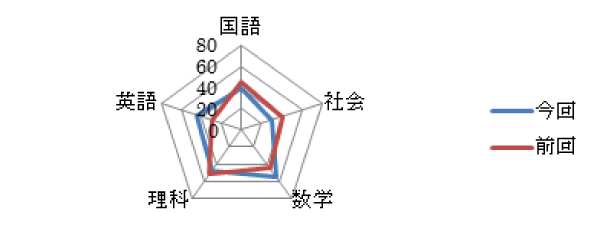
③今回の成績とこれまでの成績
・偏差値による成績
受験したすべての回の成績を、科目別、3科目(国・数・英)、4科目(国・数・理・英)、5科目に分けて算出します。
・順位による成績
所属中学、進学区または地域、全体の受験人数と順位、そして1000人換算順位を算出します。
・5科目偏差値の動きと次回の期待偏差値
各回の成績の動きと、これからの目標レベルを示します。
④今回の志望校別成績
<国公立第1~第3希望>
・志望校順位
性別と学科内全体に分けて、その志望人数と順位を示します。
・入試科目・配点に合わせた成績
志望高校の入試科目と配点に合わせた得点と偏差値を求め、それにより志望校順位 算出や合格可能性を示します。
・合格可能性の動き
今回の合格可能性を示しています。
<合格可能性について>
A まず心配ない。上位合格のはず。
B ほぼ、安全圏。合格の多くはこの学力層
C ボーダーゾーン。合否は五分五分。
D 危険率が高く、発奮が必要。
E 志望校の再考が必要。
K 予測困難(データ不足、志望者が極めて少ない高校等)
合格可能性の様子
【成績から推測する標準内申点】
成績から推測して、これ位の内申点が標準というものです。
五ツ木書房に蓄積されたデータを分析して示しています。
公立入試では、学力検査の成績と内申点の両方で合否が決められます。
今回の成績と標準内申点の両方で合格可能性がどうなるかを示します。
⑤今回のあなたの成績から志望校をピックアップ
志望校とは別に、今回の成績からの適正校をピックアップしてくれます。
【例】サンプル
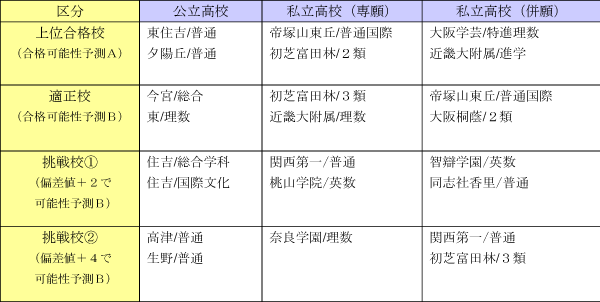
⑥採点済答案用紙
実際に採点したあなたの答案をすべて掲載しています。間違った部分の復習に活用できます。
⑦学習アドバイス
今回の成績と誤答傾向を分析して、アドバイスをしています。具体的な勉強方法、弱点の指摘など、成績アップへの近道を示しています。
⑧志望校の情報
今回志望した高校の過去年度の入試データを示したものです。
過去2年間の募集人数、応募人数、合格人数、競争率が分かります。
また、主な併願先の高校名も示してくれます。
⑨項目別得点率
今回のテストの項目別得点率を教科別にレーダーチャートのグラフで表しています。
⑩小問別成績
項目をさらに細かく分け、各小問ごとに出題内容と正誤を示しています。
結果(個人成績表)はどう見ればいいの?-合格判定編-
個人成績表に、どんな内容が書かれているか、お分かりいただけたかと思います。
それでは、その結果をどう見れば良いのでしょうか?
表の見方を含め、例をご紹介させていただきます。
【偏差値について】
高校選びの基準として用います。
下記のコラムで詳しく説明していますのでそちらも参考ください。
【合格可能性と、その信憑性について】
50年以上も実施してきた実績がありますから、データの信憑性は高いと言えます。
ただし、この記号の判定「だけ」に捉われないようにした方が良いです。
「A、B判定がでたから、もう安心」
「C、D判定だから、もう合格できない」
と、簡単に判断してしまう声はよく聞きます。
記号で最も分かりやすい指標になるため、ここだけに目がいってしまいがちになります。
ただし、よく考えてみてください。上記コラム「高校選びと偏差値の関係について」で、
「5科目偏差値を3上げる場合の目安は、およそ5科目合計を25点上げる」
という内容がありました。そして、1科目につき5点アップさせるのであれば、うっかりミスを数問なくすだけでクリアできる範囲です。
一概には言えませんが、偏差値が3変われば、D判定がC判定に、C判定がB判定に変わる可能性は十分にあります。逆に、B判定でも、うっかりミスが増えれば、あっという間にC判定に下がります。
E判定に関しては、確かに現在の実力と志望校に大きなギャップがあるかもしれません。
極端な話、偏差値が40で、志望校の偏差値が60だと差が大きすぎます。
ただ、上記のように、D判定までは比較的上がりやすいところにいる可能性はあります。そうなると努力次第でC判定以上が見えてきます。
また、判定を上げるためには、あと何点必要かも一緒に記載されています。
例えば、C判定が出たとして、よく見ると「Bまであと1点」ということもあります。
5科目で1問だけ正解が増えればクリアできます。
よって繰り返しになりますが、この記号の判定「だけ」に捉われないようにしましょう。
K判定に関しては、普通は出ることは、ほとんどありません。
近畿圏外を志望校として出した場合は、データが少なくて出ることがあります。
大切なことは、判定の記号に一喜一憂することではなく、結果を次にどう活かすか、ということです。
結果(個人成績表)はどう見ればいいの?-データ分析編-
まず前提として、模試は1回だけ受けるのではなく、複数回受けた方が良いです。少なくとも、3回は受けるようにしましょう。
1回だけでは、必ず偏りが生じます。得意分野が多く出題されたら、得点が取れるでしょうし、苦手分野ばかりがでてしまったら、得点は取れなくなります。その1回だけの結果で、大切な志望校を決めてしまうのは危険です。
また、時期としては9・10・11月が望ましいです。既に述べましたが、年間を通して最も受験者数が多く、信憑性のあるデータが取れるためです。
・教科バランスを見る
自分自身の、強みと弱みをしっかり把握してください。
【例】
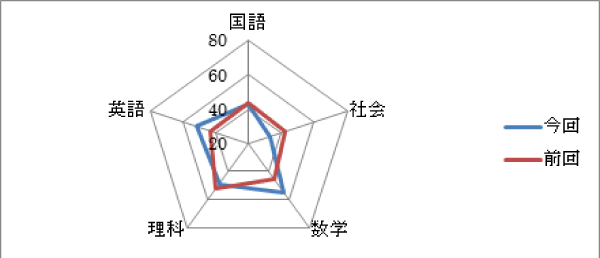
※初めて受けた場合は、今回のみの記載になります。
分かりやすい様に、少し極端な例にしました。
グラフの形が正五角形に近い程、科目間の偏差値の差が少なく、バランスが良いと言えます。5科目均等にできたことに越したことはないですが、苦手科目があっても、得意科目でしっかりカバーできていれば問題ありません。
また、「前回」と「今回」の差をしっかりと見てください。
目盛りが、前回より下がっているか、同程度か、上がっているか、を見るだけで構いません。
- (例)国語、理科
前回と今回で、偏差値がほぼ同等です。
良く言えば、安定していると言えますが、悪く言えば現状維持と言えます。
苦手な分野を克服すれば、まだまだ上がる可能性があります。 - (例)数学、英語
前回と比較して、今回は偏差値が大幅に上がっています。
偏差値は上がっていれば嬉しいものですが、注意が必要です。それは、「なぜ上がったのか?」の分析を行うことです。
シンプルに以下の2パターンに分けて考えます。A:「勉強をしたから上がった」
B:「勉強はしなかったが上がった」Aの場合は、努力の成果が出たと言えます。
ただし油断せずに、ケアレスミスがなかったかどうかのチェック、苦手分野や問題のやり直しをしっかりとしてください。
「上がったから良かった」で済ましてしまうと、そこに落とし穴があります。それについては以下で触れます。Bは要注意です。
これは、「たまたま」上がっただけの可能性が十分あります。「たまたま」には色々な要因がありますが、
1.たまたま、いつもより計算ミスが少なかった
2.たまたま、得意な分野や問題が出た
3.たまたま、勘で埋めた問題が正解した
4.たまたま、適当に記号問題を埋めたら正解した上記のどれかに当てはまったら要注意です。
本当の意味で、科目の実力がアップした、とは言い切れないからです。Aの場合でも、この「たまたま」は起こりえます。
なので、しっかりと見直しをするようにしましょう。 - (例)社会
前回と比較して、下がっていることが分かります。
これも、上記で述べた「前回が、たまたま良かった」か、どうかを分析する必要があります。
ただ、社会は暗記要素の強い科目ですから、この場合は苦手分野が多く出題された可能性が高いです。特に、歴史は得意だけど、今回は苦手な地理が多く出題された。
また、歴史だけで言えば、鎌倉・室町時代は好きだけど、江戸時代は苦手、などといったパターンです。これらを踏まえた上で、それを明確にするために、次に項目別得点率を確認してください。
・項目別得点率について
例えば上記の例では、数学の偏差値が大きく上がっていました。
しかしながら、細かく分析をかけることで、より今後の成績アップを目指すことが可能です。【例】
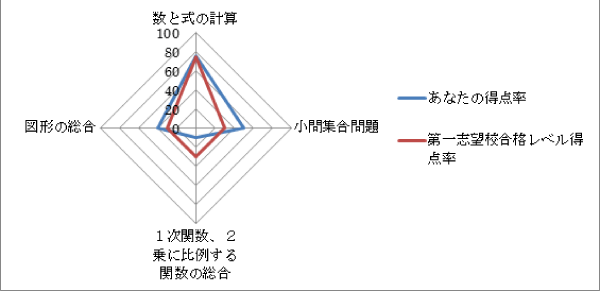
数と式の計算
合格レベルに達しているので、適正と分かります。小問集合問題、図形の総合
合格レベルよりも得点が取れているので優秀です。1次関数、2乗に比例する関数の総合
合格レベルよりも大幅に低い結果と言えます。
「関数」の分野が苦手ということが分かりますので、徹底して復習する必要があります。「偏差値が上がったから良かった」で済ましてしまうと、ここを見落としがちになります。
もしも、この苦手分野を中心に問題が出題されると、たちまち点数が取れなくなってしまうので要注意です。逆に、偏差値が下がってしまった場合や、判定が悪かった場合でも、分野によれば、合格レベルに達しているかしれません。こういった場合でも、上記のように、苦手分野をしっかりと確認して復習しましょう。
まとめ
五ツ木模試は、学校のテストだけでは測れない、偏差値という現在における自分の位置を知る絶好の機会です。
また、他の受験生と一緒に受けることにより、試験本番の雰囲気を味わうこともできます。
それだけでも収穫はありますが、それ以上に大切なことは、入試本番に向けて、次の勉強にそれをどう活かすか、ということです。
五ツ木模試を最大限に活かして入試に備えましょう。


