勉強の仕方アドバイス
「数学だけはどうも苦手…。」「正直、数学は諦めている」
という生徒は多いかもしれません。なぜなら、中学生に苦手な教科で、常に上位ランクインするのが数学だからです。中学3年生になって受験勉強をするようになっても、数学が苦手な生徒はなかなか数学の勉強がはかどらず、他の教科の勉強ばかりしてしまいがち。しかし、中学数学が身に付いていないと高校に行っても苦労することになってしまいます。そうならないためにも、まずは偏差値50を目指しておきたいところです。今回はそんな数学に苦手意識がある受験生に向けて、偏差値50以上を取るための中学数学の勉強法を紹介します。
目次
偏差値50とは?
そもそも偏差値50って何??という方のために、簡単に説明しておくと、偏差値50とは、あるテストで平均点を取った人がもらえるポイントのことです。
偏差値を出すには複雑な計算をしなければならないので、そのあたりのところは省略しますが、もしも平均点が60点のテストで、あなたが60点を取れば「偏差値50」となります。
苦手としている数学において、平均点をとるのはなかなか大変そうな気がしますが、正しい方法で勉強をすれば必ず平均点は取れます。
実は基礎を固めるだけで平均点は取れる
入試問題においては基礎をしっかりと固めることで、平均点を取ることができます。
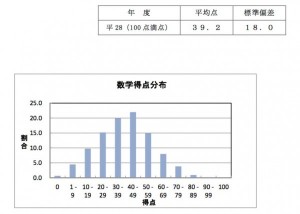
一例として、滋賀県公立高校入試(平成28年度)における数学の平均点を見てみましょう。
(平成28年度滋賀県立高等学校入学者選抜結果のまとめについて)
平均点は39.2点となっています。
この年度の入試の場合、もしあなたが40点を取っていたら偏差値50以上になる、というわけです。
平均点がとても低いような気がしますが、裏を返せばそれだけ難しいテストなのです。
しかし、よくよく問題を見ていくと、問題によって「基礎的な問題」と「応用問題」に分かれています。
https://www.kyoto-np.co.jp/common/dld/pdf/9398512bad48cf8b5b2e729820803c1b.pdf
大問1〜4に分かれていますが、大問1は基礎レベルの問題ばかりになっています。大問1では計10問出題されており、この配点を見ると42点となっています。
つまり、大問1を全問正解できれば、平均点(39.2点)を上回り、偏差値50以上となるわけです。
偏差値50というと、数学を苦手としている人には高いハードルのように感じられますが、基礎をしっかりと固めることで偏差値50を取ることができるのです。
基礎を固めるにはどうしたらいいの?
意外に思うかもしれませんが、数学の基礎的な問題は「暗記」です。数学というと、思考力・論理力が問われるようなイメージがあると思います。確かにその通りなのですが、それは応用レベルの問題になってからの話で、基礎レベルの問題は暗記で乗り切ることができます。
何を暗記するのかと言えば「解き方の暗記」です。
数学の基礎レベルの問題は、解き方の手順を暗記することで正解にたどり着くことができます。
このことは駅までの道順を暗記するのと同じです。
例えば、自宅から駅までの道順が、
1. 家を出て東へ100m進む
2. 郵便局の角を右に曲がる
3. コンビニの角を左に曲がる
4. 駅につく
という行き方だったとします。
この道順を覚えていないと、駅にたどり着くことができません。
数学の場合もこれと同じで、例えば「二次方程式」の解き方の場合、
1.「左辺=0」の形にする
2.因数分解できる場合は、左辺を因数分解して解く
3.因数分解できない場合は、解の公式を使って解く
といった手順で問題を解いていきます。
この手順を覚えることができていなければ、正解にたどり着くことができません。
数学が苦手な人は、この手順のどこかが抜けていたり、手順の途中でミスをしていることに気づいていないので、正解にたどり着くことができません。
右に曲がるところで、左に曲がっているようなものです。
ここでは例として二次方程式を挙げましたが、関数にしても図形にしても、それぞれ解き方の手順があります。
手順の通りに作業をすすめていけば、必ず正解にたどり着くことができるのです。
ですから、まずはそれぞれの解き方の手順をしっかりと暗記してしまいましょう。
解き方の手順は学校や塾の先生に聞いたり、手順を丁寧に解説している参考書を見たりすれば、すぐに知ることができます。
効率の良い暗記方法についてはコチラ!⇒勉強で効果的な暗記方法はありますか?
長期記憶に残す方法についてはコチラ!⇒これで半年後も忘れない!受験で活かせる暗記のコツを伝授します。
解き方の手順の暗記ができたら?
解き方の手順の暗記ができたら、実際に解いてみましょう。駅までの道順の例で言えば、実際に駅まで行ってみることが大切です。
「解き方が分からない」といって質問に来てくれた後で、実際に自分で解かない人がいます。
解説を聞いてできるようになったつもりになっているのですが、これは道順だけ聞いて、実際に歩いてみないのと同じです。
しばらく時間が空くと「あれ??郵便局の角を左に曲がるんだっけ??右だっけ??」となってしまいます。
解き方の手順が暗記できたら、次は実際に解いてみることが大切です。
最後は繰り返しの回数できまる!
解き方の暗記ができて、さらに実際に解いてみて正解にたどり着くことができたとします。
正解にたどり着くことができると、そこで安心してしまいがちなのですが、まだまだ油断は禁物です。1回解いただけでは忘れてしまうからです。
コンビニの角を左に曲がるつもりをしていても、間違えてスーパーの角を左に曲がってしまうかもしれません。
それは繰り返しの反復練習が足りていないからです。確実に正解にたどり着くためには、繰り返しの練習が必須なのです。
みなさんの自宅までの道順は「○○を右に曲がって、次は○○を左に曲がって・・・」みたいに意識しなくても、自然に帰ることができると思います。
いわば、頭を使わずに“反射的に”帰ることができますよね。
それは何度も何度も同じ道を通っているからできるのです。ほぼ毎日繰り返しているからこそ、できるのです。
数学においても、確実に正解にたどりつくためには、正しい手順で何度も繰り返し反復練習重ねることが重要なのです。
反復練習を繰り返して、基礎レベルの問題を“反射的に”正解にたどりつくことができるようになれば、偏差値50はとることができます。
応用問題は基礎問題の組み合わせでできている
さらに、基礎を固めることができれば、応用問題を解くための下地ができあがっています。
偏差値50を超えて、さらに上を目指していくためには応用問題を避けて通ることはできません。
しかし、応用問題とはいっても基礎問題の組み合わせでできている場合がほとんどです。
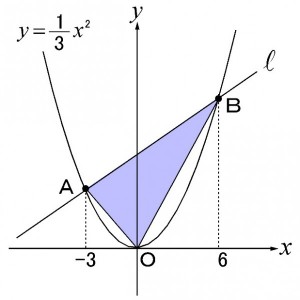
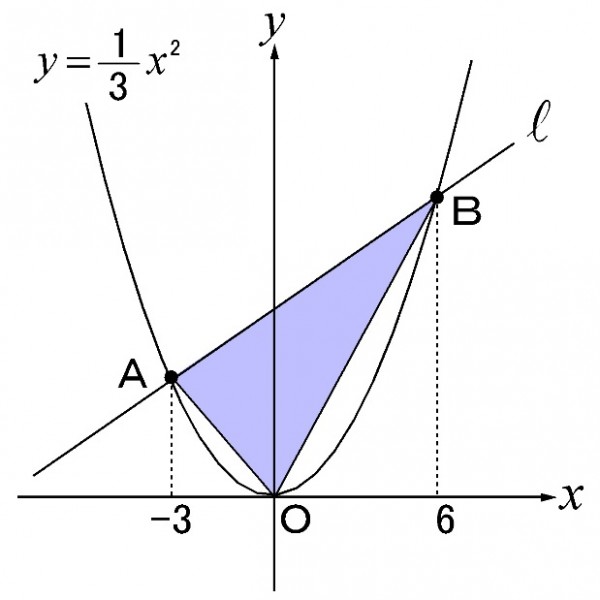
例えば「色のついた部分の三角形の面積を求めなさい」という問題。
この場合、
・三角形の面積の求め方 ・グラフの交点の座標の出し方 ・一次関数の式の求め方 ・二次関数の式の求め方
これらの知識の組み合わせで解くことができます。
基礎レベルの知識が身に付いていれば、その組み合わせで応用問題を解くことができるのです。
まとめ
数学が苦手な中学生のために、偏差値50以上を取るための勉強法をお伝えしてきました。
偏差値50は基礎レベルの問題をすべて正解すれば、取ることができます。
基礎レベルの問題は、解き方の暗記をすることで正解できるようになります。
応用問題は基礎レベルの問題の組み合わせでできているので、
まずは基礎レベルの問題を解けるようになることを目指せば、自然に偏差値50以上が取れるようになります!